When you take out a loan, you know that you need to repay the money you borrowed with some interest, but how does it work and what does it mean? In this blog we will go through an example and answer the questions.
You borrow some money.
You borrow £5,000 with an interest rate of 10% per year. Youdon’t make any repayments and then pay the money back after a year. How muchmoney would you have to pay? Firstly, you must pay £5,000 to cover the amountwe borrowed. You would then need to pay 10% of £5,000, which equals £500, ininterest. This means that you would have to pay back £5500.
But what if you borrowed the money for two years?
The interest rate you got was per year. So, if you borrowedfor two years, you would have to pay two years’ worth of interest. You mightthink that means you would have to pay back £6,000 (£5,000 for the loan, £500for the first year’s interest and £500 for the second year’s interest), butunfortunately it doesn’t work like that.
At the end of the first year, you owe £5,500, that means atthe start of year 2 you have effectively borrowed £5,500. This would mean thatat the end of the second year you would need to pay back the £5,500 from thefirst year and 10% interest on this amount (which equals £550), this means thatafter two years you would have to pay back £6,050.
If you did this for five years, you would end up having topay back £8,052!
This is called compound interest. It’s where you payinterest on the interest. You can imagine what happens if you keep not payingthe loan back; you end up paying interest on interest on interest on interest…
But interest on loans isn’t normally charged annually
Whilst you might see interest advertised on an annual basis,it is usually charged daily or monthly. You divide the annual interest rate by12 to calculate the monthly interest rate, and 365 to get the daily rate. A 10%annual interest works out as a monthly interest rate of 0.83%.
How much would you have to pay back if you borrowed £5,000for two years with interest charged monthly?
At the end of the first month there would be 0.83% intereston £5,000; this works out to £41.67 interest. In the second month there wouldbe 0.83% interest on £5,041.67; this works out to £42.02 interest. You can seethat the interest is compounding. In the graph we show how the interest isgrowing in each month:
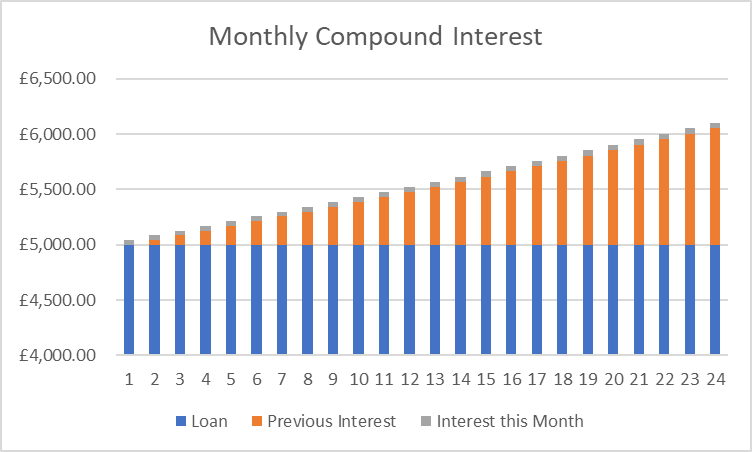
In the first month you can see the loan amount of £5,000 (bluebar) and a small amount of interest (grey bar). In the second month the loan isthe same amount, but you now have interest from the previous month, theinterest this month is also slightly larger than last month. In month 12 you can see that the interest is much larger (in fact the interest this month is nearly 25% larger than in the first month).
To pay this loan off after 2 years would cost you £6,102. This is £50 more than if the interest was calculated annually.
If you kept this loan for 5 years before paying it back, it would cost us £8,227. This is £174 more than if the interest was annual. This means that the actual interest rate you paid is higher than the 10% annual rate. The actual interest rate we paid is called the APR. Check out our blog on understanding APR to learn more.
If the interest were calculated daily, it would cost us even more.
But normally you make repayments each month
Let’s assume that instead of borrowing the money and waiting five years before paying anything back, you made a repayment each month of£106.24. What happens then. The graph shows the first month:
For the first month you have borrowed £5,000 (dark blue) andyou would owe £41.67 (orange bar) of interest. So, after the first month youwould owe the bank £5,041.67. You then make a repayment of £106.24 (green bar).This leaves an outstanding balance of £4,935.43 (light blue bar).
The opening balance in the second month would be £4,935.45.On this you would pay £41.12 interest and make a repayment of £106.24. Thiswould leave an outstanding balance of £4,870.32.
In the second month you paid £0.50 less interest and insteadused this to further repay your loan.
That didn’t make that much difference
£0.50 in a month is not a lot of difference, but in the sameway that interest on interest adds up, not paying interest on a small part ofthe loan quickly makes savings. The more your repayment is going towards theloan, and not interest, the quicker the savings come. You can see this in the nextgraph which shows the percentage of each month’s repayment that is paying off yourloan vs paying off interest:
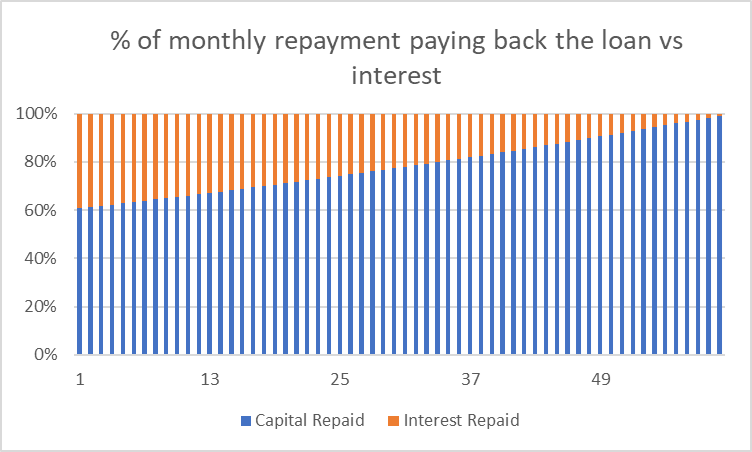
In the first month 40% of your repayment is paying offinterest whereas in the last month 1% of your repayment is paying interest.
Earlier we said that if you had not made any repayments andpaid loan and interest back at the end, you would pay £8,227. Paying it backover 5 years costs you £6,374 (£106.26 per month * 60 month). This saves you £1,853compared to paying it all back at the end.
What would happen if you could afford higher loan repayments?
If you had some spare money in your budget and could affordrepayments of £161 per month then you could pay the loan off in 3 years. Theinterest in the first month would be the same as before (£41.67) but the extramoney you are repaying would reduce the loan further. This means that in thesecond month the interest would only be £40.67. This is £0.50 less than when yourepaid it over 5 years. This means that in the second month more of your moneyis repaying the loan and not paying interest.
We can now see that only 26% of the repayment is paying offthe interest in the first month. In each month more of your money is payingback your loan and less is paying interest.
In fact, paying off the loan in 3 years would cost you £5,808.This saves you £566 compared to smaller monthly payments over 5 years. Not onlydoes it save you money but after 3 years the money you were using for the loanis yours to spend as you wish!
But remember not to over-estimate what you can afford, sometimeslife throws an unexpected expense your way.
Your creditscore will be affected if you fail to make a payment, making futureborrowing (including getting a mortgage) more expensive.
